As we are entering the era of Big Data, everyone and their moms seem to be talking about PCA. All the papers you read mention PCA (with lots of jargon, of course). Half of the seminars you’ve been to this month touch on PCA. Your boss/collaborators suggest trying PCA on your data.
“What is this PCA thing that keeps running into me?” You ask.
Short for principal component analysis, PCA is a way to bring out strong patterns from large and complex datasets. For example, if you measure the expression of 15 genes from 60 mice, and the data come back as a 15×60 table, how do you make sense of all that? How do you even know which mice are similar to one another, and which ones are different? How do you know which genes are responsible for such similarities or differences?
PCA might be what you need to untangle that data mess. What it does is to take the expression data of 15 genes from each mouse and smoosh them down to one single dot that represents the expression profile of that mouse. One dot for one mouse. Sixty mice, sixty dots. The result will look like this:
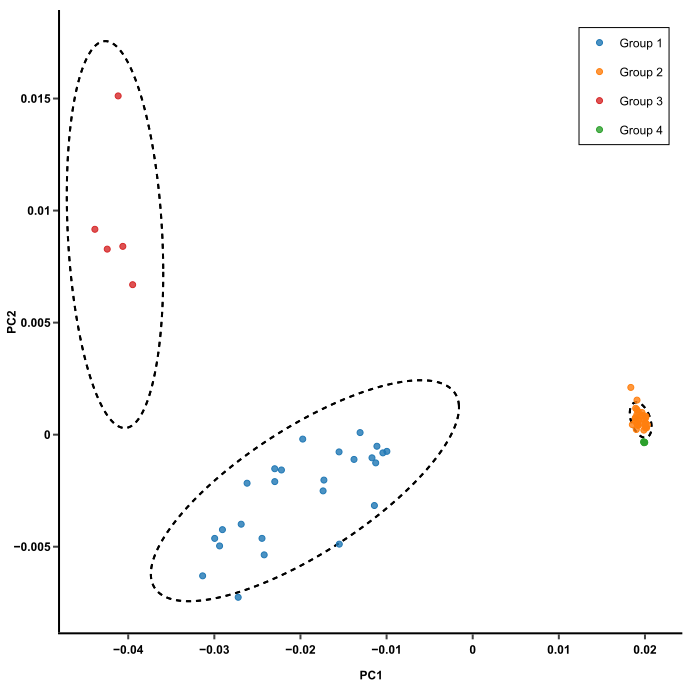
This plot makes it much easier to compare mice. Those with similar expression profiles will cluster together. In this plot, there are 3 clusters of mice. From here, you can trace back to find out which genes make the clusters different from one another (more on that later).
Neat! How do we go from that 15×60 table to this pretty plot?
1. Principal components capture the most variation in a dataset
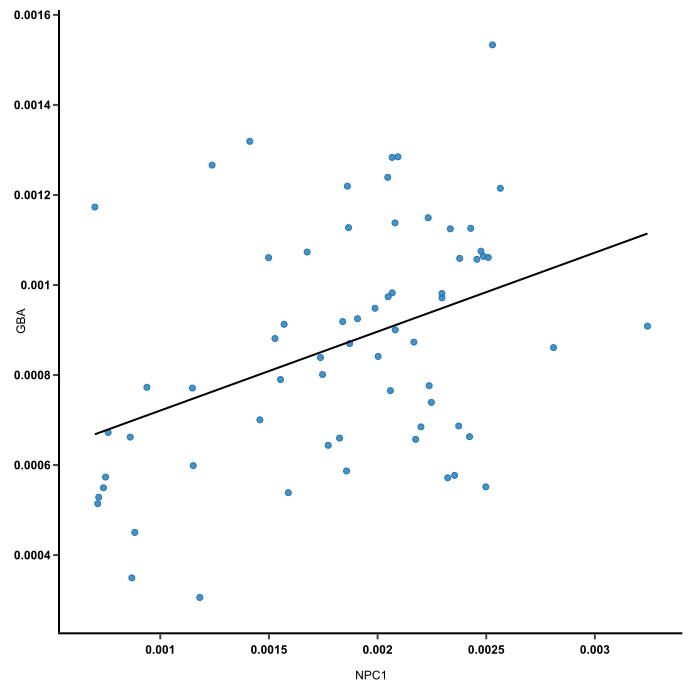
Let’s not forget that what we are trying to do here, from the moment that the 15×60 table arrives and we stare at it in bewilderment, is to compare the mice. When there are too much information about them, it’s hard to do that. Let’s start with 2 genes to make things easier. Using those 2 genes as axes, we can plot their expression in 60 mice on a 2D plot, like this:

Here, each dot carries read counts of 2 genes from one mouse, and together they form a flat “cloud.” Principal component 1 (PC1) is a line that goes through the center of that cloud and describes it best. It is a line that, if you project the original dots on it, two things happen:
- The total distance among the projected points is maximum. This means they can be distinguished from one another as clearly as possible. We want to compare stuff, remember? If a line blurs data points together, it won’t help.
- The total distance from the original points to their corresponding projected points is minimum. This means we have a representation that is as close to the original data as possible.
In other words, the best line — our PC1 — must convey the maximum variationamong data points and contain minimum error. These two things are actually achieved at the same time, because Pythagoras said so.
2. PCA deals with the curse of dimensionality by capturing the essence of data into a few principal components.
But we have 15 genes, not just 2. The more genes you’ve got, the more axes (dimensions) there are when you plot their expression. When it gets to about the fourth gene, you probably don’t want to plot this anymore, let alone 15 genes. 15 genes equal 15 axes! The cloud of dots is no longer flat, it is 15-D now. There is no way to look at it and make any sense out of it.
This is when the magic of PCA comes in. To create PC1, a line is anchored at the center of the 15-D cloud of dots and rotate in 15 directions, all the while acting as a “mirror,” on which the original 60 dots are projected. This rotation continues until the total distance among projected points is maximum. The rotating line now describes the most variation among 60 mice, and is fit to be PC1.
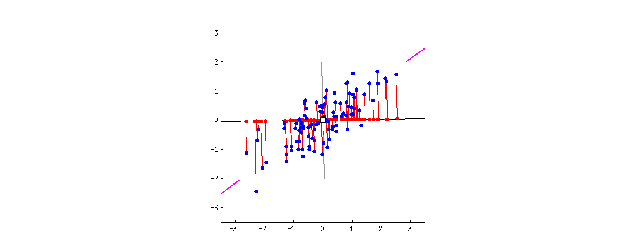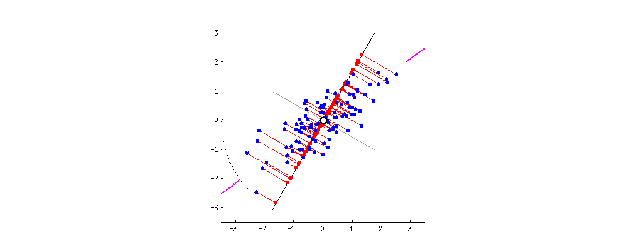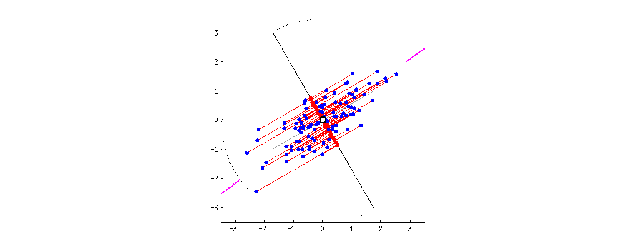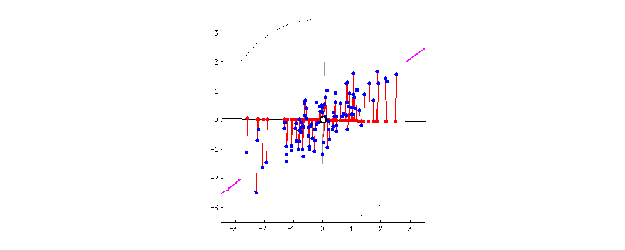
Source: stats.stackexchange.com
PC2 is the second line that meets PC1, perpendicularly, at the center of the cloud, and describes the second most variation in the data. (Computers can handle all this rotation and setting up PCs in a breeze, lucky us!)
If PCA is suitable for your data, just the first 2 or 3 principal components should convey most of the information of the data already (more on this later). This is nice in several ways:
- Principal components help reduce the number of dimensions down to 2 or 3, making it possible to see strong patterns.
- Yet you didn’t have to throw away any genes in doing so. Principal components take all dimensions and data points into account.
- Since PC1 and PC2 are perpendicular to each other, we can rotate them and make them straight. These are the axes of our pretty PCA plot.
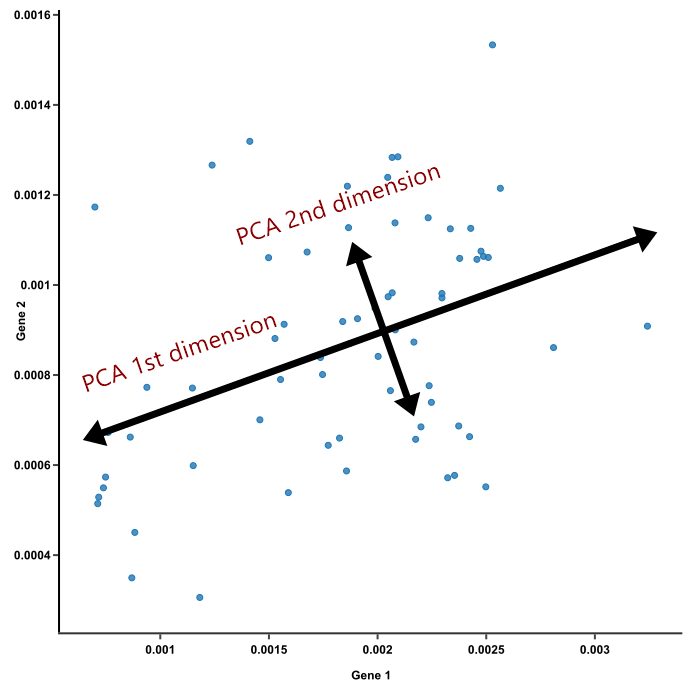
3. Dimensions vary in the weights they have on each principal component.
Now that we have the axes, how about dots? How do we smoosh 15 genes together to create a single dot for each mouse?
The original dots (mouse gene expression) are pinned in place by their values on all axes (genes). These dots are projected on PC lines, which are trying to stay as close as possible to all the dots — that’s how they achieve the best fit. For the PC lines, this is like trying to stand still while being pulled in 15 directions at once. Some pulling forces are stronger than others; in other words, dimensions have different weights in defining each PC.
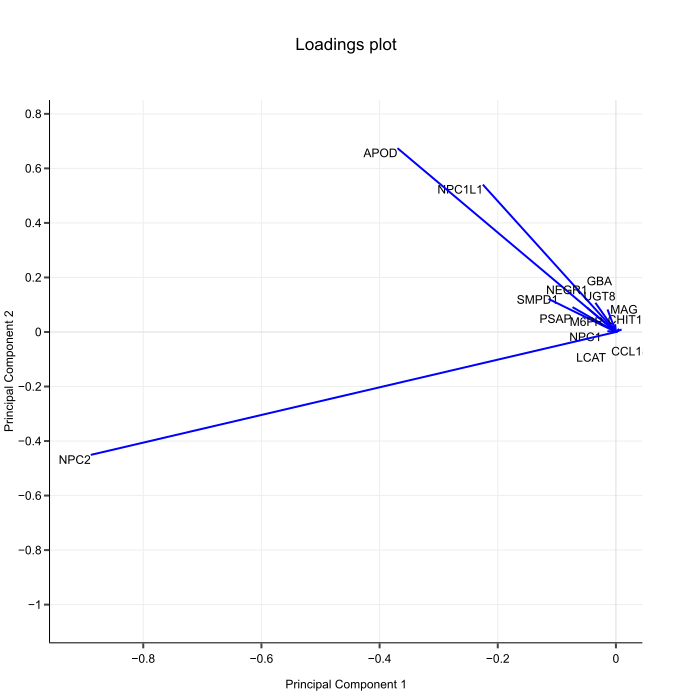
In our example, all 15 genes participate in placing mice on PCs, but they weigh in differently. After their weights are determined, finding out where they put Mouse #1 on PC1 is simple math:
(gene1 read count * gene1 weight on PC1)
+ (gene2 read count * gene2 weight on PC1)
+ …
+ (gene15 read count * gene15 weight on PC1)
= PC1 value of Mouse #1
Mouse #1 has a spot on PC2, too. To calculate it, use the same formula with weights of genes on PC2 instead of PC1.
With a value of PC1 and a value of PC2, Mouse #1 now can be graphed as a dot on the PCA plot.
This simple math can be written in a fancy formula that’s more appropriate for papers and seminars:
Let,
- Mouse #i :
- Eigenvector #j:
- Principal component j-th of sample i:
Do this math again on all the mice, and they will each become a dot on the PCA plot.

Pretty! How do we read this?
4. How to read a PCA plot
- Mice that have similar expression profiles are now clustered together. Just glancing at this plot, we can see that there are 3 clusters of mice.
- If 2 clusters of mice are different based on PC1, like the blue and orange clusters in this plot, such differences are likely to be due to the genes that have heavy influences on PC1.
- If 2 clusters are different based on PC2, like the red and blue clusters, then the genes that heavily influence PC2 are likely to be responsible.
- Keep in mind that PCs are ranked by how much they describe the data. PC1 reveals the most variation, while PC2 reveals the second most variation. Therefore, differences among clusters along PC1 axis are actually larger than the similar-looking distances along PC2 axis.
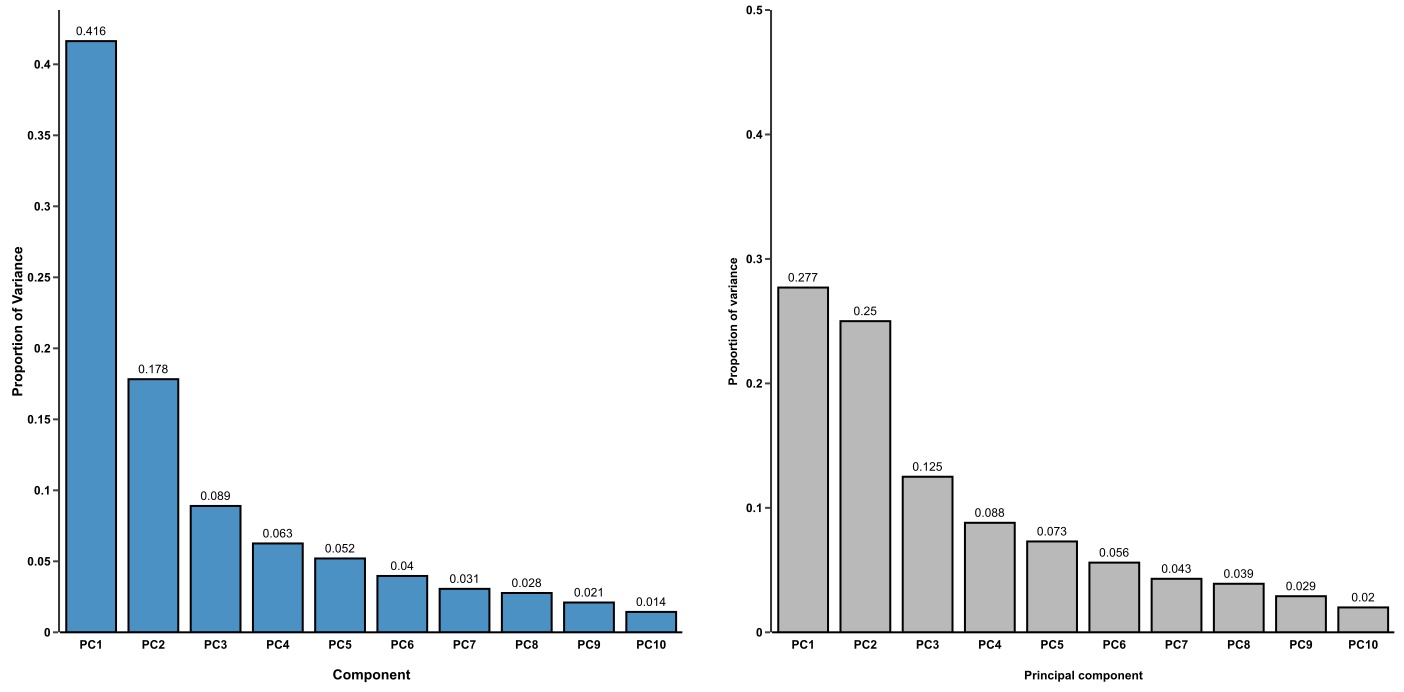
- Is this plot meaningful? Check the proportion of variance, or the diagnostic scree plot. PCA is worthy if the top 2 or 3 PCs cover most of the variation in your data. Otherwise, you should consider other dimension reduction techniques, such as t-SNE and MDS.
To sum up, principal component analysis (PCA) is a way to bring out strong patterns from large and complex datasets. The essence of the data is captured in a few principal components, which themselves convey the most variation in the dataset. PCA reduces the number of dimensions without selecting or discarding them. Instead, it constructs principal components that focus on variation and account for the varied influences of dimensions. Such influences can be traced back from the PCA plot to find out what produces the differences among clusters.
To run a PCA effortlessly, try BioVinci. This drag-and-drop software can perform any statistical analyses in just a few clicks. Check it out here: https://vinci.bioturing.com
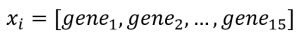
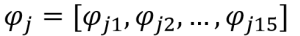
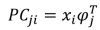
Stan
I like the article
Md Mahmudul Hasan
Excellent explanation! Loved this! Thank you!
Tien
Hi Hasan. Thank you for the kind words. We updated a post on 3D PCA as well, check it out here: https://blog.bioturing.com/2020/10/12/the-why-when-and-how-of-3d-pca/
Confused PhD researcher
Brillant Thanks!
Tien
We updated a post on 3D PCA as well, check it out here: https://blog.bioturing.com/2020/10/12/the-why-when-and-how-of-3d-pca/. If you have questions in other topics, please share with us, we’d love to help.
Jeff Buckthal
Best description I have ever seen. Thank you!
Carolina Cozzi
I just used your tool to create a PCA, it´s very easy !!
I only have one question, how do i know which samples are present in the cluster.. it does not tell me.
Can you help me?
Ingrid
a question: is there a requirement for the minimum size of the data set for application of PCA to make sense?
Anna
Incredibly well-described! I’ve finally understood PCAs! Thank you so much 🙂
Peter enis
Cool
Jane Doe
I think credit to the actual person who created the rotating plot would be more appropriate than just “stats.stackexchange.com” https://stats.stackexchange.com/a/140579/343377